Answer:

Explanation:
To find the coordinates of the point that partitions in a 1:3 ratio, we use:
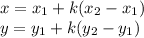
Where
 is the ration of partitions,
is the ration of partitions,
 in this case.
in this case.
Now, we replace all values:
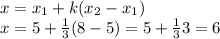
So, the horizontal coordinate is 6.
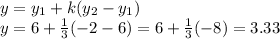
The vertical coordinate is 3.33.
Therefore, the coordinates of the point that partitions the directed line segment AB in a 1:3 ratio is
