Answer:
Hence, g(x) is inverse of f(x)
Explanation:
The provided function are f(x)=5x-25 and
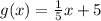
To check g(x) is the inverse of f(x)
Plug the formula for g(x) into every instance of "x" in the formula for f (x):
(fog)(x) = f(g(x))
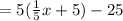
= x+25-25
= x
Now, plug the formula for f (x) into every instance of "x" in the formula for g(x) :
(gof)(x) = g(f(x))
=
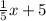
=
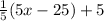
= x - 5 + 5
= x
Both ways we get "x"
So, both functions are inverse of each other.
Hence, g(x) is inverse of f(x) .