For this case we have to define trigonometric relationships in rectangular triangles that:
The sine of an angle is given by the opposite leg to that angle on the hypotenuse of the triangle.
Then, according to the figure shown we have to:
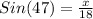
So, clearing the value of "x" we have:
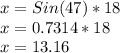
We round and we have the value of "x" is:

Answer:
