Question

A company that manufactures racing boats estimates that the profit for selling its brand is given by the following equation.

P(b) = -25b3 + 750b2 + 2,500b

What is the least number of racing boats, b, that must be manufactured to make a profit of $75,000?

Answer 1

`b = 10`

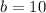
Explanation:

`P(b) = -25b^3 + 750b^2 + 2500b`

This equation shows the income obtained based on the number of boats sold. We want to know the minimum number of boats that must be sold to obtain $ 75 000.

Then we must equalize the equation to 75 000 and clear b.

3 solutions will be obtained (because it is a polynomial of degree 3), and the lowest value will be taken.

`P(b) = 75000`

`-25b^3 + 750b^2 + 2500b = 75000`

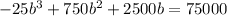
Now we need to solve the equation, for that we seek to factor the polynomial

`-25b^3 + 750b^2 + 2500b - 75000 = 0`

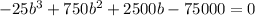
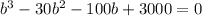`b^3 -30b^2 - 100b + 3000 = 0` we divide the equation by -25

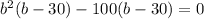`b^2(b-30) - 100(b-30) = 0` We take common factor b

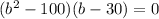`(b^2 -100)(b-30) = 0` We take out common factor (b-30)

Finally the solutions are:

`b = 30\\\\b^2 -100 = 0\\\\b^2 = 100`

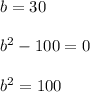
b = 10 and b = -10

We take the least positive solution (because you can not produce -10 boats)

Finally b = 10

The smallest number of boats that must be produced to make a profit of $ 75,000 is 10 boats.