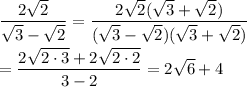Question

What is the simplest form of 2 √2 / √3 - √2?

A.) 2√6 + 4
B.) 2√5 + 4
C.) 2√6+4 / 5
D.) 2√5+4 / 5

Answer 1

The answer is A.

Explanation:

I just did it

Answer 2

A.) 2√6 + 4

Explanation:

The reason for the direction to use a conjugate to rationalize the denominator is that multiplying by the conjugate lets you take advantage of the factoring of the difference of squares:

(a +b)(a -b) = a² -b²

When "a" or "b" involves a square root, this will eliminate the radical.

So, you have ...

`(2√(2))/(√(3)-√(2))=(2√(2)(√(3)+√(2)))/((√(3)-√(2))(√(3)+√(2)))\\\\=(2√(2\cdot 3)+2√(2\cdot 2))/(3-2)=2√(6)+4`