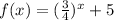Question

What function equation is represented by the graph? f(x)=(43)x+5 f(x)=(34)x+5 f(x)=(43)x+6 f(x)=(34)x+6

Answer 1

B

Explanation:

Answer 2

Option B is correct.

`f(x) = ((3)/(4))^x+5`

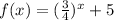
Explanation:

Exponential function: An exponential is of the form:
`f(x) = ab^x`

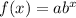
where a is the initial value and b is the growth factor

If b> 1, then the function is an exponential growth function.

if 0<b< 1 , then the function is an exponential decay function.

The function which is represented in the graph is exponential decay function.

The parent function
`f(x) = ((3)/(4))^x` represents the exponential function.

Vertical shift:

If c is a positive real number , then the graph y= f(x)+c is the graph of y =f(x) shifted c units upward.

If c is a positive real number , then the graph y= f(x)-c is the graph of y =f(x) shifted c units downward.

Then;

The graph
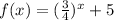`f(x) = ((3)/(4))^x+5` is the graph of
`f(x) = ((3)/(4))^x` is shifted 5 units up.

Therefore, the function which represented in the graph is
`f(x) = ((3)/(4))^x+5`