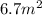Question

A parallelogram has sides measuring 23.8 m and 35.3 m. The height corresponding to the 23.8-m base is 9.9 m. Find the height, to the nearest tenth of a meter, corresponding to the 35.3-m base.

Answer 1

The value of x i.e DE is
`6.7m^2`

Explanation:

Given a parallelogram has sides measuring 23.8 m and 35.3 m. The height corresponding to the 23.8-m base is 9.9 m. we have to find the height corresponding to the 35.3-m base which is DE

Area of parallelogram ABCD=
`Base AB* heightDE`

=
`35.3* x`

=
`35.3x m^2`

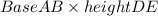
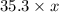
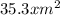
Area of parallelogram ABCD=
`Base BC* heightDF`

=
`23.8* 9.9`

=
`235.62 m^2`

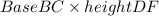
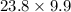
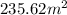
Above two is the area of same parallelogram

⇒
`35.3x=235.62`

⇒
`x=6.6747\sim6.7m^2`

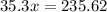
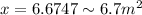
Hence,The value of x i.e DE is
`6.7m^2`