Question

Rewrite the function in standard form, intercept form, find the vertex, find the y-intercept, and find the x-intercepts.

Please show your work

y=(x+4)^2-1

Answer 1

Standard form - y=x^{2}+8x+15

Intercept form - y=(x+5)(x+3)

The vertex is is (-4,-1)

y intercept=(0,15)

X intercepts (-5,0) and (-3,0)

Explanation:

The given quadratic equation is

`y=(x+4)^(2) -1\\y=x^(2)+8x+16-1\\y=x^(2)+8x+15`

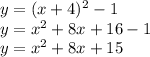
and we know that the standard form of the quadratic equation is

`y=ax^(2)+bx+c`

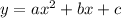
so on comparing with it the above is the standard form only and also we can get the value of a (coefficient of
`x^(2)`) and b( coefficient of x) and constant c so we get them as follows

a=1, b=8 c= 15 now ac=16 so the two numbers whose product is 15 and add is 8 are 5,3

so writing the equation in the Intercept form is
`y=(x+5)(x+3)`

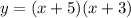
now lets find the vertex,now recall that all parabolas are symmetrical. This means that the axis of symmetry is halfway between the x−intercepts or their average.

axis of symmetry
`=(-5-3)/(2)=(-8)/(2)=-4`

This is also the x−coordinate of the vertex. To find the y−coordinate, plug the x−value into either form of the quadratic equation. We will use Intercept form.

`y=(-4+5)(-4+3)=-1`

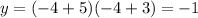
so, the vertex is (-4,-1).

now Vertex form is written as
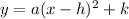`y=a(x-h)^(2)+k` , where (h,k) is the vertex and a is the same as in the other two forms.

for Y intercept put x=0 in the given vertex form

y=
`(0+4)^(2)-1=16-1=15`

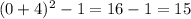
y intercept=(0,15)

for X intercept put y=0 in intercept form

`0=(x+5)(x+3)`

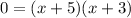
X intercepts (-5,0) and (-3,0)

Answer 2

y = x^2 + 8x + 15 the standard form.

y +1 = (x + 4)(x + 4) intercept form.

Vertex = (-4, -1)

y-intercept is (0, 15)

x-intercept are (-3, 0) and (-5, 0)

Explanation:

The given equation is in vertex form.

y = (x + 4)^2 - 1

To write in standard form, we have to expand the above function.

Here we use the formula (a + b)^2 = a^2 + 2ab + b^2

y = x^2+ 2*4*x + 4^2 - 1

y = x^2+ 8x +16 - 1

y = x^2 + 8x + 15 the standard form.

y +1 = (x + 4)(x + 4) intercept form.

Vertex = (h, k) = (-4, -1)

y-intercept

To find the y-intercept, plug in x =0 in the above equation.

y = (0 + 4 )^2 -1

y = 16 - 1

y = 15

y-intercept is (0, 15)

x-intercept

To find the x-intercept plug in y =0 and find the values of x.

(x + 4)^2 -1 =0

(x + 4 )^2 =1

Taking the square root on both sides, we get

x + 4 = ±1

x-intercept are (-3, 0) and (-5, 0)

Hope this will helpful.

Thank you.