Question

Rewrite the function in standard form, intercept form, find the vertex, find the y-intercept, and find the x-intercepts.

Please show your work

f(x)=(x+3)^2-4

Answer 1

We have the function,
`f(x)=(x+3)^(2)-4`

On simplifying, we get,

`f(x)=x^2+6x+9-4`

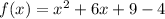
i.e.
`f(x)=x^2+6x+5`

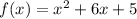
Thus, the standard form of the function is
`f(x)=x^2+6x+5`.

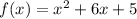Now, the factors of the given functions are (x+1) and (x+5).

Since, the intercept form of the function is the factored form of the function.

So, we have, intercept form of the function is
`f(x)=(x+1)(x+5)`.

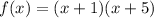Now, we know that,

Value of x-coordinate of the vertex is
`(-b)/(2a)` i.e.
`(-6)/(2* 1)` i.e.
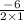`(-6)/(2)` i.e. x= -3

Then,
`f(-3)=(-3)^2+6* (-3)+5` i.e.
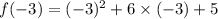`f(-3)=9-18+5` i.e. f(-3)=-4

So, the vertex of the function is (-3,-4).

Further, we know that, 'the y-intercept of a function is the point where the function crosses y-axis'.

So, when x=0, we have,
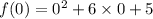`f(0)=0^2+6* 0+5` i.e. f(0) = 5

Thus, the y-intercept is (0,5)

Also, 'the x-intercept of a function is the point where the function crossese x-axis'.

Then, for f(x)=0, we have
`0=x^2+6x+5` i.e.
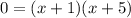`0=(x+1)(x+5)` i.e. x= -1 and x= -5

Thus, the x-intercept are (-1,0) and (-5,0).