We're generating a sequence of functions
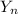 with
with
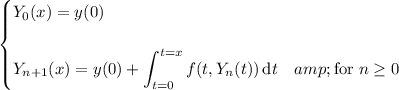
where
 , so that the sequence
, so that the sequence
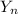 converges to
converges to
 as
as
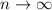 .
.
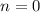 :
:
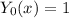
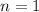 :
:
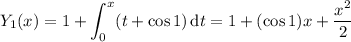
 :
:

Unless you're familiar with Fresnel integrals, you won't be able to simplify this any further.
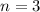 :
:
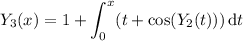
My computer takes a really long time to compute
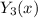 , and even longer to plot it, so I've ultimately omitted
, and even longer to plot it, so I've ultimately omitted
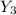 from the plot. (I wonder now if by "until to 3-th aproximation" it's intended that you only go up to
from the plot. (I wonder now if by "until to 3-th aproximation" it's intended that you only go up to
 ...)
...)
I've attached a plot of the approximations (dashed and colored) along with a more precisely computed numerical solution (black)