Answer:
the height will be maximum at 1.5
Explanation:
We have been given the function:
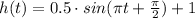
Height depends on
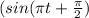
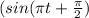
This will be maximum when value of its is 1
And value will be 1 when t=0.
So, substitute the value of t=0 in given function:
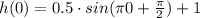
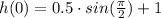
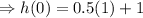
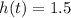
Hence, the height will be maximum at 1.5