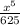Answer:
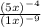 is simplified to
is simplified to
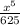
Explanation:
Consider the given expression "5x to the -4 power Over 1x to the -9 power".
We can write this mathematically as,
5x to the -4 power as
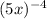
and 1x to the -9 power as
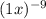
Thus, 5x to the -4 power Over 1x to the -9 power can be written as,
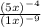
We have to simplify the above expression,
Consider,
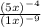
This can be re-written as,
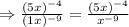
Solving further,
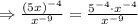 ,
,
using property of exponent,
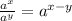
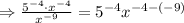 ,
,
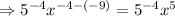 ,
,
using property of exponent,
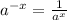
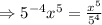 ,
,
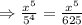
Thus,
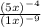 is simplified to
is simplified to