Question

What is the equation of a line that passes through the point (6, 1) and is perpendicular to the line whose equation is y=−2x−6 ?

Enter your answer in the box.

Answer 1

y = 1/2x - 2

Look at Desmos Math pic i sent.

Answer 2

y =
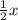`(1)/(2) x` + 3

Explanation:

To find the equation that passes through the points (6,1) and is perpendicular to the line whose equation is y = -2x - 6, we are going to follow the steps below;

First, we determine the slope of the equation:y = -2x - 6, only then can we find the slope of our perpendicular equation.

y = -2x - 6

m = -2

The slope of the above line is -2

So, the slope of the perpendicular line to y = -2x - 6 will have a slope equals to the negative reciprocal , that is;
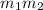`m_(1) m_(2)` = -1

The slope(m) of our perpendicular equation is
`(1)/(2)` using the above formula.

Haven gotten our slope, next is for us to find our intercept

To get the intercept, we will use this standard equation;

y = mx + c

where m =slope(our new slope=1/2) c=intercept x and y are the two points through which the line passes through. That is; x=6 and y=1. So we are going to plug in all this variable into the standard equation;

y = mx + c

1 =
`(1)/(2)`(6) + c

1 = 3 + c (six will divide two to give us three)

To get the value of c, subtract 3 from both-side of the equation

1 - 3 = 3+ c -3

-2 = c

c = -2

Therefore, our new intercept is 3

So we can now plug in our new slope and intercept into y=mx+c

y =
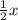`(1)/(2) x` + 3

We can re-arrange it;

-
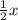`(1)/(2) x` + y = 3