Question

What is the equation for a geometric sequence with a first term of 4 and a second term of −12? an = 4(−3)n − 1 an = 4(3)n − 1 an = 4(36)n − 1 an = 4(−36)n − 1

Answer 1

Option 1
`a_n = 4(-3)^(n-1)`:

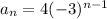Explanation:

The geometric sequences have the following form:

`a_n = a_1(r)^(n-1)`

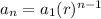
Where
`a_1` is the first term in the sequence

We know that the first term is 4

Then
`a_1` = 4

We also know that the second term is -12

Then
`a_2 = -12`

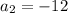
We know that in geometric sequences the relationship between consecutive terms is constant. So:

r = -12/4

r = -3

Finally the general formula of this sequence is:

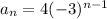`a_n = 4(-3)^(n-1)` Option 1