Answer:
[1].
Option A and D are correct.
[2].
Option A is correct
Explanation:
[1].
Quadratic function states that it is an equation of second degree i.,e it contains at least one term that is squared.
The standard form of the quadratic equation is;
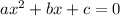
A.
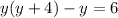
Using distributive property:
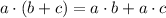
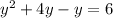
Combine like terms;

or
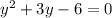 which represents a quadratic equation.
which represents a quadratic equation.
B.
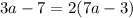
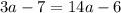
or
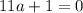 which is not a quadratic equation.
which is not a quadratic equation.
C.
(3x+2)+(6x-1) = 0
Combine like terms;
9x +1 = 0 which is not a quadratic equation.
D.
4b(b) = 0
 which represents the quadratic equation.
which represents the quadratic equation.
[2].
Given the parent function:
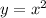
The reflection rule over x axis is given by;
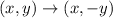
then
the function become:
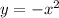
Vertical shift:
If c is a positive real number, the graph y=f(x)+c is the graph of y =f(x) shifted upward c units.
If c is a positive real number, the graph y=f(x)-c is the graph of y =f(x) shifted downward c units.
then;
The graph
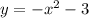 is the graph of
is the graph of
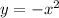 shifted 3 units down.
shifted 3 units down.
Therefore, the translation of the graph of
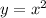 to obtain
to obtain
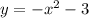 is, reflect over the x-axis and shift down 3
is, reflect over the x-axis and shift down 3