Answer:
D. $31,337.27
Explanation:
We have that the initial amount of the loan is $5500.
Miranda took the loan for 4 years. So, the total present value is $5500×4 = $22,000.
The rate of interest on the loan is 7.5% i.e. 0.075 and it was for the duration of 10 years.
Also, it is given that the loan was compounded annually.
We have the formula as,
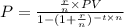
i.e.
![PV=(P* [1-(1+(r)/(n))^(-t* n)])/((r)/(n))](https://img.qammunity.org/2020/formulas/mathematics/middle-school/qe4rfhv4ehplzu4zlknz97rcjimm7ofzt2.png)
Substituting the values, we get,
i.e.
![PV=(P* [1-(1+(0.075)/(12))^(-10* 12)])/((0.075)/(12))](https://img.qammunity.org/2020/formulas/mathematics/middle-school/59ctgft4vf8sznh85yv5b4sk94os40pwaj.png)
i.e.
![22000=(P* [1-(1+0.00625)^(-120)])/(0.00625)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/6ep8salfnzop7lgudq2ievxk8k12jjk2va.png)
i.e.
![22000=(P* [1-(1.00625)^(-120)])/(0.00625)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/haybattus6s2f6m991s7m6ub1juhvwo043.png)
i.e.
![22000=(P* [1-0.4735])/(0.00625)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/vuq5w1yyspi8lhpi8mdcbk24i5t4vucm31.png)
i.e.
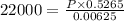
i.e.
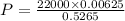
i.e.
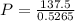
i.e.
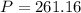
Thus, the total lifetime cost to pay of the loans compounded annually = 261.16 × 120 = $31,339.2
Hence, the total cost close to the answer is $31,337.27