Question

Can you help me on my math homework

Answer 1

1. w = -6, -7

2. v = -3, 11

3. Frame's width all around is same, x, and x = 1 inch

4. The other zero of the function is 5 ( x = 5 )

Explanation:

1.

For the question given
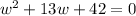`w^2+13w+42=0` , we need to find 2 numbers such that their sum is equal to the number before x (which is 13) and their product is equal to the constant (which is 42) AND THEN replace 13w with those 2 numbers(and w).

Such two numbers are 7 and 6

Now we can write:

`w^2+7w+6w+42=0`

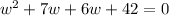
Then we can group the first 2 terms and last 2 terms and take common, then solve.

`w^2+7w+6w+42=0\\w(w+7)+6(w+7)=0\\(w+6)(w+7)=0`

Since two expressions' product is equal to 0, either w+6 = 0 or w+7 = 0

w+6=0

w = -6

and

w+7 = 0

w= -7

Hence, w = -6, -7

2.

This is similar to Question #1, so we need two numbers that multiplied gives us -33 and added gives us -8.

Such two numbers are -11 and +3

Thus we can replace -8 with this and take common and then solve for v:

`v^2-8v-33=0\\v^2+3v-11v-33=0\\v(v+3)-11(v+3)=0\\(v-11)(v+3)=0`

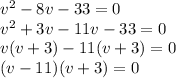
So either v-11 =0 or v+3 = 0

v - 11 = 0

v = 11

and

v+3=0

v = -3

Hence, v = -3, 11

3.

Since total area of frame & photo is 120, we need an expression for frame & photo and equate that to 120.

If picture's width is 10 and two sides there is frame of x inches each, so width of whole this is 10 +2x

Similarly, the length is 8 and two sides there is frame of x inches each, so length of whole is 8 +2x

Area of rectangle is length * width

Thus, we have
`(10+2x)(8+2x)=120`

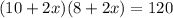
We need to find x, so we solve the equation above:

`(10+2x)(8+2x)=120\\80+20x+16x+4x^2=120\\4x^2+36x+80-120=0\\4x^2+36x-40=0\\x^2+9x-10=0\\x^2+10x-x-10=0\\x(x+10)-1(x+10)=0\\(x-1)(x+10)=0\\x=1, -10`

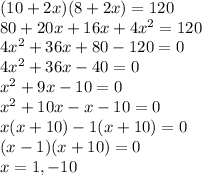
Since length cannot be negative, x = 1 only

4.

Factoring the original equation as we did earlier, we see "what two numbers multiplied gives us -35 and added gives us +2?"

Those 2 numbers are +7 and -5

Thus we can write, group, and solve for x:

`x^2+2x-35=0\\x^2+7x-5x-35=0\\x(x+7)-5(x+7)=0\\(x-5)(x+7)=0`

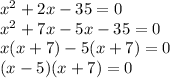
So x-5 =0 or x+7 = 0

x+7=0

x = -7 (already given in the problem)

and

x-5=0

x=5

Hence, the other zero of the function is 5

Answer 2

QUESTION 1

The given equation is

`w^2+13w+42=0`

Split the middle term to get;

`w^2+7w+6w+42=0`

Factor to get,

`w(w+7)+6(w+7)=0`

We factor further to obtain,

`(w+7)(w+6)=0`

Apply the zero product property to get,

`(w+7)=0\:or\:(w+6)=0`

`w=-7\:or\:w=-6`

QUESTION 2

The given equation is

`v^2-8v-33=0`

Split the middle term to get;

`v^2-11v+3v-33=0`

Factor to get,

`v(v-11)+3(v-11)=0`

We factor further to obtain,

`(v-11)(v+3)=0`

Apply the zero product property to get,

`v-11=0\:or\:v+3=0`

`v=11\:or\:v=-3`

QUESTION 3

The length of the photo is
`l=10 in.`

The width of the photo is
`w=8 in.`

The length of the frame is
`L=10+2x in.`

The width of the frame is
`W=8+2x in.`

The area total area of the frame is
`=(10+2x)(8+2x) in^2`

The total of the frame of the photo must be 120.

This implies that,

`(10+2x)(8+2x)  =120`

`\Rightarrow (10+2x)(8+2x) -120=0`

We rearrange and simplify to get,

`\Rightarrow 4x^2+20x+16x+80-120=0`

`4x^2+36x-40=0`

We divide through by 4 to obtain;

`x^2+9x-10=0`

Split the middle term

`x^2+10x-x-10=0`

Factor

`x(x+10)-1(x+10)=0`

`(x+10)(x-1)=0`

`x=-10\: or\:1`

Since x is length,
`x=1`

The dimensions of the frame are

`L=10+2(1) =12in.`

`W=8+2(1) =10in.`

QUESTION 4

`f(x)=x^2+2x-35`

Equate the function to zero

`x^2+2x-35=0`

Split the middle term

`x^2+7x-5x-35=0`

Factor

`x(x+7)-5(x+7)=0`

`(x+7)(x-5)=0`

`(x+7)=0,(x-5)=0`

`x=-7,x=5`

Hence the other zero is 5