Question

Find an equation of the line having the given slope containing the given point slope -9 through (1,-8)

Answer 1

y = - 9x + 1

Explanation:

the equation of a line in slope- intercept form is

y = mx + c ( m is the slope and c the y-intercept )

here m = - 9, hence

y = - 9x + c ← is the partial equation

To find c substitute (1 , - 8) into the partial equation

- 8 = - 9 + c ⇒ c = - 8 + 9 = 1

y = - 9x + 1 ← equation of line

Answer 2

y + 8 = -9(x-1)

Explanation:

Pre-Solving

We are given that a line has a slope of -9 and contains the point (1,-8).

We want to write the equation of this line.

The equation of this line can be written in three ways:

• Point-slope form, which is
  `y-y_1=m(x-x_1)`, where m is the slope and
  `(x_1,y_1)` is a point.
• Standard form, which is ax+by=c, where a, b, and c are free integer coefficients.
• Slope-intercept form, which is y=mx+b, where m is the slope and b is the value of y at the y intercept.

Either one of these ways works, but let's use point-slope form, as that form is the easiest.

Solving

We can immediately substitute the values into the formula to get the equation.

We can start with the slope; replace m with -9 in the formula.

`y-y_1=m(x-x_1)` =>
`y-y_1=-9(x-x_1)`

We can now replace
`x_1` and
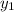`y_1` with 1 and -8 respectively.

y - -8 = -9(x-1)

This can be simplified to:

y + 8 = -9(x-1)