Answer:
k = 5
n = 10
p = 0.5
Explanation:
Let X be a discrete random variable. The binomial probability formula is used to calculate the probability of obtaining k-successes in "n" independent trials for an experiment with probability of success p and probability of failure q.
The binomial formula is the following:
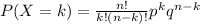
Where:
k = number of successes
n = number of trials
p = probability of success
q = probability of failure.
So, for the given problem
k = 5 Because you want to get the probability of getting 5 "heads"
n = 10 Because the experiment is repeated 10 times
p = 0.5 Because the probability of obtaining a "heads" when flipping a coin is 50%
q = 0.5