Question

What is the arc length of the arc sub tended in a circle with radius 6 and an angle of 7 pi/ 8

Answer 1

Formula for the Arc length is given by:

`\text{Arc length} = 2 \pi r \cdot (\theta)/(360^(\circ))`

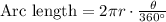
As per the statement:

radius of circle(r) = 6 units

Angle (
`\theta`) =
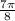`(7 \pi)/(8)` radian

Use conversion:

`1 rad = (180)/(\pi)`

`(7 \pi)/(8)` =
`(180)/(\pi) \cdot (7 \pi)/(8) = (1260)/(8) = 157.5^(\circ)`

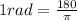
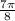then;

substitute these given values we have;

Use value of
`\pi = 3.14`

`\text{Arc length} = 2\cdot 3.14 \cdot (6) \cdot (157.5^(\circ))/(360^(\circ))`

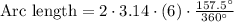
or

`\text{Arc length} = 2\cdot 3.14 \cdot (6) \cdot 0.4375`

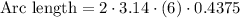
Simplify:

`\text{Arc length}=16.485`

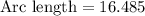
Therefore, the arc length of the arc substended in a circle with radius 6 units an angle of 7 pi/8 is 16.485 units