Answer:
Value of x is 17.5.
Explanation:
Consider the figure given below,
Given : A triangle RST with measure of ∠R= 80° and PQ ║ TS.
RP = 8, PT = 14, RQ= 10 , QS = x
We have to find the value of QS.
Consider ΔRTS AND ΔRPQ,
∠R= 80° =∠R (Common)
PQ ║ TS and RT is transverse, ∠P = ∠T (Alternate angles)
Thus, ΔRTS ≅ ΔRPQ (by AA similarity)
By CPCT,
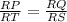
Substitute values above, we get,
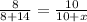
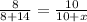
Solve for x, we get,
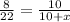
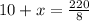
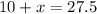
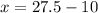
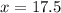
Thus, value of x is 17.5.