Question

Analyze the diagram below and complete the instructions that follow solve for x

Answer 1

Value of x is 17.5.

Explanation:

Consider the figure given below,

Given : A triangle RST with measure of ∠R= 80° and PQ ║ TS.

RP = 8, PT = 14, RQ= 10 , QS = x

We have to find the value of QS.

Consider ΔRTS AND ΔRPQ,

∠R= 80° =∠R (Common)

PQ ║ TS and RT is transverse, ∠P = ∠T (Alternate angles)

Thus, ΔRTS ≅ ΔRPQ (by AA similarity)

By CPCT,

`(RP)/(RT)=(RQ)/(RS)`

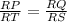
Substitute values above, we get,

`(8)/(8+14)=(10)/(10+x)`

`(8)/(8+14)=(10)/(10+x)`

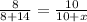
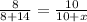
Solve for x, we get,

`(8)/(22)=(10)/(10+x)`

`10+x=(220)/(8)`

`10+x=27.5`

`x=27.5-10`

`x=17.5`

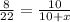
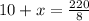
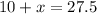
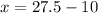
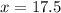
Thus, value of x is 17.5.

Answer 2

Option C. x = 17.5

Explanation:

As we know If two triangles are similar then they follow SAS, SSS or AA property(any one). Now from the given image both the triangles will be similar if the two sides of the triangles are in the same ratio and angle between these two sides are same.

Given size of one side = 8+14 =22

Size of other side = 10+x

and the common angle between these lines is 80°.

Now we apply the property of similarity

⇒
`(10)/(10+x) = (8)/(22) \\`

Now we cross multiply the fractions on each side

⇒ 8(10+x) = 22×10

⇒ 80+8x = 220

⇒ 8x = 220-80

⇒ 8x = 140

⇒ x =140÷8

x = 17.5