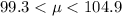Question

Use the given information to construct a 95% confidence interval estimate of the mean of the population. n = 62, σ = 11.4, = 102.1

A. 101.7 < μ < 102.5

B. 66.1 < μ < 138.1

C. 100.7 < μ < 103.5

D. 99.3 < μ < 104.9

Answer 1

`99.3<\mu<104.9`

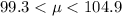
Therefore, option D is correct.

Explanation:

We have been given
`n=62,\sim=11.4\text{and}\bar{x}=102.1`

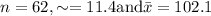
The formula to find interval is:
`\mu` which is unknown mean.

`\bar{x}\pm(\sim)/(√(n))\cdot \text{z-score}`

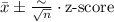
So, 95% confidence interval is standard value of z-score at 95% confidence interval is 1.96

Substituting the values in the formula we will get:

`102.1/pm(11.4)/(√(62))(1.96)`

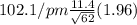
On simplifying the above equation we will get:

Taking
`102.1-(11.4)/(√(62))(1.96)=99.26≈99.3`

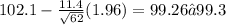
and
`102.1+(11.4)/(√(62))(1.96)=104.93`

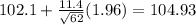
Therefore, option D is correct.

`99.3<\mu<104.9`