Question

Spencer hits a tennis ball past his opponent. The height of the tennis ball, in feet, is modeled by the equation h(t) = –0.075t2 + 0.6t + 2.5, where t is the time since the tennis ball was hit, measured in seconds. How long does it take for the ball to reach the ground?

Answer 1

Hence it takes 11.02 seconds for the ball to reach the ground.

Explanation:

Spencer hits a tennis ball past his opponent. The height of the tennis ball, in feet, is modeled by the equation
`h(t)=-0.075t^2+0.6t+2.5`, where t is the time since the tennis ball was hit, measured in seconds.

We have to find the time taken by the ball to reach the ground

i.e. we have to find the value of t such that height is zero i.e. h(t)=0.

`h(t)=-0.075t^2+0.6t+2.5=0`

or it can be rewritten as,

`-0.075t^2+0.6t+2.5=0`

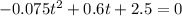
we now find the roots of the above quadratic equation.

`0.075t^2-0.6t-2.5=0`

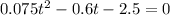
multiply both side by 1000,

`75t^2-600t-2500=0`

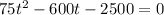
Solve using Quadratic formula,

For a given quadratic equation ax^2+bx+c=0 we can find roots using,

x=\frac{-b\pm\sqrt{b^2-4ac}}{2a} ...........(1)

Here, a = 75 , b= -600 , c= -2500

`t=(-\left(-600\right)\pm √(\left(-600\right)^2-4\cdot \:75\left(-2500\right)))/(2\cdot \:75)`

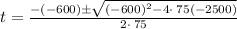
On solving , we get

`t=(2\left(6\pm√(111)\right))/(3)`

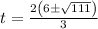
on solving the equation we get two roots as:

t= - 3.02377 and t= 11.0238

As time can't be negative; hence we will consider the value of t as t= 11.0238.

Hence it takes 11.02 seconds for the ball to reach the ground.