Answer:
Option 1 -
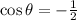
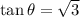
Explanation:
Given :
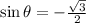 and
and
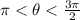
To find : What are the values of
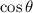 and
and
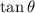 ?
?
Solution :
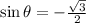
We know,
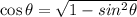
Substitute the value of
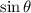 ,
,
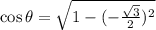
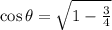
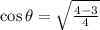
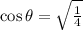
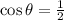
Since,
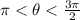 i.e. in third quadrant
i.e. in third quadrant
We know,
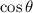 in third quadrant is negative.
in third quadrant is negative.
So,
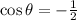
Now,
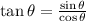
Substitute the value of
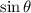 and
and
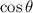 ,
,
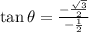
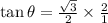
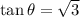
We know,
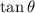 in third quadrant is positive.
in third quadrant is positive.
So,
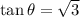
Therefore, Option 1 is correct.