Question

The Polygons below are similar find the value of x and y

Answer 1

`x=49\degree,y=6`

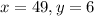
Explanation:

Angle
`x` corresponds to the complement of the
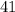`41\degree` in the bigger triangle. See diagram in attachment.

This implies that,

`x=90-41=49\degree`

Also since the triangles are similar, the sides are in the same proportion.

This implies that,

`(3y-8)/(15)=(4)/(6)`

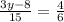
We multiply both sides by 15 to get,

`3y-8=(4)/(6)* 15`

`\Rightarrow 3y-8=(2)/(3)* 15`

`\Rightarrow 3y-8=10`

`\Rightarrow 3y=10+8`

`\Rightarrow 3y=18`

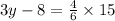
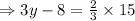
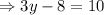
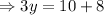
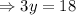
We divide through by 3 to get,

`y=6`

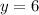
The correct answer is D