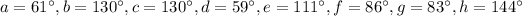I've redrawn and labeled the given image. Angles
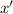 are supplementary to angles
are supplementary to angles
 ; that is, for any angle
; that is, for any angle
 ,
,
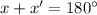
It's also useful to know that for any convex
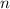 -gon, the sum of its interior angles is
-gon, the sum of its interior angles is
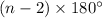
Notice that the angle supplementary to the one labeled
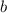 is congruent to the angle supplementary to the one labeled
is congruent to the angle supplementary to the one labeled
 ; this means that
; this means that
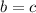 .
.
So we have
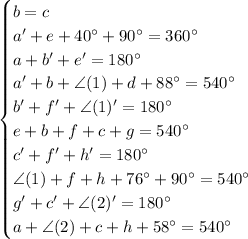
Solving the system will give you