Question

A rock of mass 200 g is attached to a 0.75 m long string and swung in a vertical plane.

a) What is the slowest speed that the rock can travel and still maintain a circular path?
b) What is the tension in the string at the bottom of the swing?

Answer 1

Hello!!
The correct answer would be number B)!! I took the test hope it helps

Answer 2

Hello!

a) Assuming this is asking for the minimum speed for the rock to make the full circle, we must find the minimum speed necessary for the rock to continue moving in a circular path when it's at the top of the circle.

At the top of the circle, we have:

- Force of gravity (downward)

*Although the rock is still connected to the string, if the rock is swinging at the minimum speed required, there will be no tension in the string.

Therefore, only the force of gravity produces the net centripetal force:

`\Sigma F = F_g\\\\F_c = F_g\\\\(mv^2)/(r) = mg`

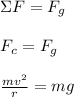
We can simplify and rearrange the equation to solve for 'v'.

`(v^2)/(r) = g\\\\v^2 = gr\\\\v = √(gr)`

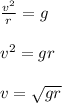
Plugging in values:

`v = √(9.8 * 0.75) = \boxed{2.711 m/s^}`

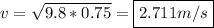
b)
Let's do a summation of forces at the bottom of the swing. We have:
- Force due to gravity (downward, -)

- Tension force (upward, +)

The sum of these forces produces a centripetal force, upward (+).

`\Sigma F = T - F_g\\\\F_c = T - F_g\\\\(mv^2)/(r) = T - mg`

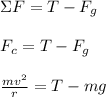
Rearranging for 'T":

`T = (mv^2)/(r) + mg\\\\`

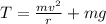
Plugging in the appropriate values:

`T = ((0.2)(2.711^2))/((0.75)) + 0.2(9.8) = \boxed{3.92 N}`