Let's call
g = acceleration on earth
g '= acceleration on the moon.
We know that:
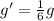
1. The formula for vertical velocity on earth is:

On the moon, we have:
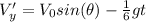

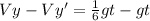
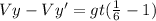
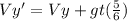
The vertical speed on the moon is greater than on earth by a factor of gt (5/6)
2. The formula for the time of flight on earth is:
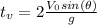
On the moon it is:
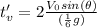
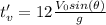
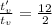
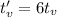
The time of flight on the moon is 6 times greater than on earth.
3. The maximum height on earth is:
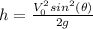
On the moon:
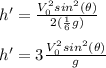
So:
![(h')/(h) = ([3(V_0^2sin^2(\theta))/(g)])/([(V_0^2sin^2(\theta))/(2g)])](https://img.qammunity.org/2020/formulas/physics/middle-school/jgxv2kizthfn7xy67jmm5o2qz1nuzf4szt.png)
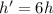
The maximum height on the moon is 6 times greater than on earth.
4. On earth, the horizontal distance traveled is equal to:
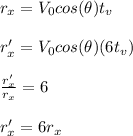
The horizontal distance traveled on the moon is 6 times greater than that of the earth.