Answer: 28 %
Explanation:
Volume of a work = productivity × time × number of workers
Let V be the initial volume of the work , x is the initial productivity , n is the initial time and w be the initial number of workers.
Then, V = x × t × n ------ (1)
When, the volume of construction work was increased by 60%, productivity of labor increased by only 25% and time remains same,
Let w' be the new number of workers,
Then, 1.6 V = 1.25 x × t × n' -------(2)
After dividing equation (2) by equation (1),
We get,
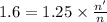

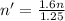
Which is the new number of workers.
Thus, the percentage increase in the number of workers =
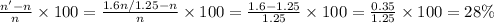
⇒The number of workers is increased by 28%.