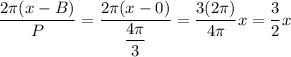Answer:
y = cos(3/2x)
Explanation:
A general sine or cosine function will have parameters of amplitude, vertical and horizontal offset, and period. The values of these parameters can be determined from the given graph.
y = A·cos(2π(x -B)/P) +C
where A is the amplitude, B and C are the horizontal and vertical offsets, and P is the period.
Amplitude
For sine and cosine functions, the amplitude of the function is half the difference between the maximum and minimum:
A = (3 -1)/2 = 1
Horizontal offset
A sine function has its first rising zero-crossing at x=0. A cosine has its first peak at x=0. The given graph has its first peak at x=0, so it is a cosine function with no horizontal offset.
B = 0
Vertical offset
For sine and cosine functions, the vertical offset is the average of the maximum and minimum values:
C = (3 +1)/2 = 2
Period
The period is the difference in x-values between points where the function starts to repeat itself. Here, we can use the peaks to identify the period as 4π/3.
P = 4π/3
Function equation
Using the parameter values we determined, the function can be written as ...
y = cos(3/2x) +2
__
Additional comment
The argument of the cosine function is ...