Answer:
Option (2) is correct.
We can write
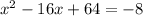 as
as
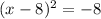
Explanation:
Consider the given equation
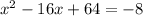
We have to rewrite it in form of identity
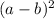
We know
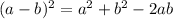
Consider the left side of the given equation,
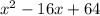
this can be written in form of
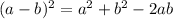
Here a = x , b = 8 , -2ab= -2 × x ×8
Then left side becomes,
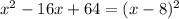
Thus , we can write
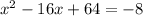 as
as
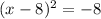
Thus, option (2) is correct.