Question

Suppose that salaries for recent graduates of one university have a mean of $25,700 with a standard deviation of $1350. Using Chebyshev's Theorem, state the range in which at least 75% of the data will reside. Please do not round your answers.

Answer 1

75% of the data will reside in the range 23000 to 28400.

Step-by-step explanation :

To find the range of values :

We need to find the values that deviate from the mean. Since we want at least 75% of the data to reside between the range therefore we have,

`1 - (1)/(k^2) =(75)/(100)`

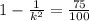
Solving this, we would get k = 2 which shows the value one needs to find lies outside the range.

Range is given by : mean +/- (z score) × (value of a standard deviation)

⇒ Range : 25700 +/- 2 × 1350

⇒ Range : (25700 - 2700) to (25700 + 2700)

Hence, 75% of the data will reside in the range 23000 to 28400.