There are 3.44 × 10²⁴ atoms in that copper rod.
Step-by-step explanation
What is the volume of the rod?
Cross-sections of this rod are circles with radius 1.15 cm. Area = π · Radius² = π · 1.15² = 4.15476 cm², which is the same along the entire rod.
Volume of the rod = Area of cross-section × Length = 4.15476 × 9.75 = 40.5089 cm³.
What's the mass of the rod?
Mass = Volume × Density = 40.5089 × 8.96 = 362.960 g.
How many moles of atoms in the rod?
The rod is made up of copper atoms. According to a modern periodic table, the atomic mass of copper is 63.55. In other words, the mass of one mole of copper atoms will be 63.55 grams. Note the unit.
Number of moles of copper atoms
= Mass of copper atoms / Mass of copper atoms in each mole
= 362.960 / 63.55
= 5.71141 moles.
How many copper atoms in that many moles of copper atoms?
By definition, there are about 6.023 × 10²³ particles in each mole of that particle. 6.023 × 10²³ is approximately the value of the Avogadro's Number,
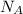. In other words,
Number of atoms
= Number of moles of atoms × Avogadro's Number.
= 5.71141 × 6.023 × 10²³
= 3.44 × 10²⁴ atoms. Rounded to three significant figures.