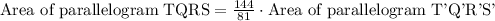Question

Find the area of each parallelogram. What is the relationship between the areas?

Answer 1

Area of parallelogram is given by:

`A = bh`

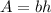
where b is the base and h is the height of parallelogram.

In parallelogram TQRS.

Coordinate of TQRS are;

T(8, 16), Q(4, 4), R(16, 4) and S(20, 16)

Coordinate of T'Q'R'S' are;

T'(2, 4), Q'(1, 1), R'(4, 1) and S'(5, 4)

Find the length of QR and PT:

Using distance(D) formula:

`D = √((x_1-x_2)^2+(y_1-y_2)^2)`

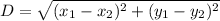
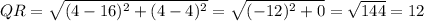`QR = √((4-16)^2+(4-4)^2) =√((-12)^2+0)= √(144)= 12` units

Similarly;

For PT:

From the graph:

P(8, 4) and T(8, 16), then

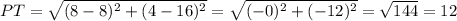`PT = √((8-8)^2+(4-16)^2) =√((-0)^2+(-12)^2)= √(144)= 12` units

In parallelogram TQRS

PT represents the height and QR represents the base of the parallelogram respectively.

then;

Area of parallelogram TQRS =
`QR \cdot PT`

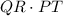
⇒Area of parallelogram TQRS =
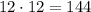`12 \cdot 12 = 144` unit square.

Now, in parallelogram T'Q'R'S'

Q'R' represents the base and P'T' represents the height of the parallelogram respectively.

here, P'(2, 1)

Find the length of Q'R' and P'T':

`Q'R' = √((1-4)^2+(1-1)^2) =√((-3)^2+0)= √(9)= 3` units

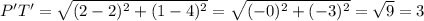`P'T' = √((2-2)^2+(1-4)^2) =√((-0)^2+(-3)^2)= √(9)= 3` units

Then;

Area of parallelogram T'Q'R'S' =
`Q'R' \cdot P'T'`

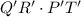
Area of parallelogram T'Q'R'S' =
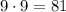`9 \cdot 9= 81` unit square.

Now, we have to find the relationship between the areas.

`\frac{\text{Area of parallelogram TQRS}}{\text{Area of parallelogram T'Q'R'S'}} = (144)/(81)`

then;

the relationship between the areas of TQRS and T'Q'R'S' is:

`\text{Area of parallelogram TQRS} = (144)/(81) \cdot {\text{Area of parallelogram T'Q'R'S'}`