Answer:
Option D.
Explanation:
The vertices of given triangle are (2,-2), (5,-2) and (2,2).
Distance formula:
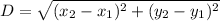
Using distance formula, the length of sides of given triangle are
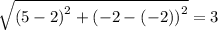
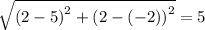
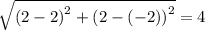
The sides of similar triangles are proportional.
Similarly, find the sides for each option.
The vertices of option D are
(2,-2), (8,-2), (2,6)
Using distance formula, the length of sides of this triangle are
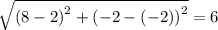
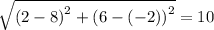
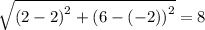
It is noticed that

Since the sides of given triangle and side of triangle in option D are proportional. Therefore, the correct option is D.