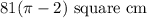Question

A circle has radius of 18 cm. Find the area of the smaller of the two regions determined by a chord with length of 18 square root of 2 cm. (Hint: Look for right triangles using Pythagorean Theorem Converse) plz help

Answer 1

Answer:
`81 ( \pi - 2)\text { square cm}`

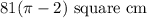
Explanation:

Let O be the radius of the circle and AB be the chord of length 18√2 cm.

Since, the radius of the circle is 18 cm,

Therefore, OA = OB = 18 cm,

Let, N be the mid point of the chord then,

AN = NB = 9√2 cm

In triangle AON,

Since,
`\angle ANO = 90^(\circ)` ( by the property of circle)

`\angle AON = sin^(-1) ((9√(2) )/(18) )`

`\angle AON = sin^(-1) ((√(2) )/(2) )`

`\angle AON = sin^(-1) ((1)/(√(2) ) )`

`\angle AON = 45^(\circ)`

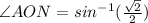
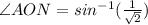
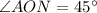
Similarly, in triangle BON,

`\angle BON = 45^(\circ)`

⇒
`\angle AOB = \angle AON +\angle BON = 45^(\circ)+45^(\circ) = 90^(\circ)`

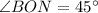
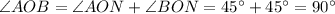
Therefore, the area of sector AOB =
`(90^(\circ))/(360^(\circ)) \pi (18)^2`

=
`(1)/(4) \pi (18)^2`

=
`81\pi \text{ square cm}`

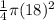
Area of triangle AOB =
`(1)/(2) * ON* AB`

=
`(1)/(2) * √(OA^2-AN^2)* AB`

=
`(1)/(2) * √(324-162)* 18√(2)`

=
`(1)/(2) * √(162)* 18√(2)`

=
`(1)/(2) * √(2)* √(81)* 18√(2)`

=
`162\text{ square cm}`

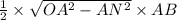
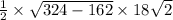
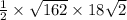
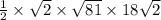
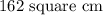
Therefore, the area of smaller region by the chord AB = Area of sector AOB - Area of triangle AOB =
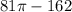
`81\pi - 162`

=
`81 ( \pi - 2)\text { square cm}`