Answer:
36 cm.
Explanation:
Let, the side of the square = x cm.
As, side of the square is 3 cm less than and 2 cm more than the sides of the rectangle.
Thus, the sides of the rectangle will be (x+3) and (x-2)
Also, it is given that, 'The area of the square is 30 cm² less than the area of the rectangle'.
As, Area of the square =

Area of the rectangle =
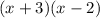
Thus, we have
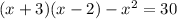
i.e.
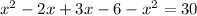
i.e.
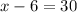
i.e.

Thus, the side of the square is 36 cm.