Answer:
20 gallons were used from the tank with the octane rating of 80.
Explanation:
Given : One tank of gasoline has an octane rating of 140 and another tank of gasoline has an octane rating of 80. To obtain a mixture of 60 gallons with an octane rating of 120.
To find : How many gallons should be used from the tank with the octane rating of 80?
Solution : Let x be the volume of gas whose octane rating is 140 and
y be the volume of gas whose octane rating is 80.
Then, we form the equation as:
(1)
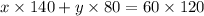

or
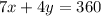 .........[3]
.........[3]
(2)
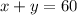
Now multiply equation (2) by 4
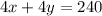 ...........[4]
...........[4]
Subtract (4) from (3)
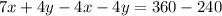
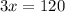
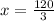
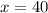
Put x in equation [4] we get,
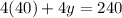
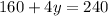
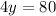
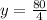
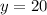
Therefore, x=40 and y=20
So, 20 gallons were used from the tank with the octane rating of 80.