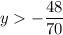The question is ambiguous, since it's not clear how we should consider the fraction. Anyway, I see two alternatives:
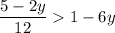
Multiply both sides by 12:

Add 72y to both sides:
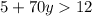
Subtract 5 from both sides:
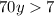
Divide both sides by 70:

If, instead, you meant
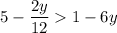
we proceed as follows: subtract 5 from both sides

Switch signs and inequality mark:
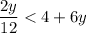
Multiply both sides by 12:
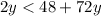
Subtract 2y from both sides:
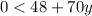
subtract 48 from both sides:
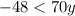
Divide both sides by 70: