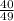Answer:
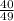
Explanation:
We are given the probabilities P(A∩B)=5/7 and P(B)=7/8 and we are to find P(A|B) according to the general equation for conditional probability.
So we will use the following formula for this:
P(A|B) = P(A∩B) / P(B)
Substituting the given values in the above formula to get:
P(A|B) =
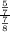 =
=
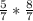
P(A|B) =