Question

Expand. (y^2 + 6)(-2y^2 + 7) =

Answer 1

-2y⁴ - 5y² + 42

Explanation:

`(y^2 + 6)(-2y^2 + 7)`

`\mathrm{Apply\:FOIL\:method}:\quad \left(a+b\right)\left(c+d\right)=ac+ad+bc+bd`

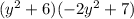
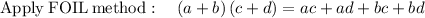
Here First terms are

`y^2 \textrm{ and } -2y^2\\(y^2)(-2y^2) = -2y^4`

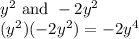
Outer terms are y² and 7 ==> (y²)(7) = 7y²

Inner terms are 6 and -2y² ==> 6(-2y²) = -12y²

Last terms are 6 and 7 ==> 6.7 = 42

So result is obtained by adding all these terms

-2y⁴ + 7y² - 12² + 42 ==> -2y⁴ - 5y² + 42

Answer 2

`\: \: \: \: \: \: \: \: \: \: \: \large\underline{\bf{ANSWER}}`

`\: \: \: \: \: \: \: \: \: \:`

`\tt↠(y^2+6)(−2y^2+7)`

`\tt↠(-2y^2+7)y^2+6(-2y^2+7)`

`\tt↠-2y^4+7y^2+6(−2y^2+7)`

`\tt↠-2y^4+7y^2-12y^2+42`

`\tt↠-2y^4-5y²+42`