Question

For the given function, find the vertical and horizontal asymptote(s) (if there are any). f(x) = the quantity x squared plus four x minus three divided by the quantity x minus six

Answer 1

Vertical asymptote at x= 6

Oblique asymptote at y=x+10

Explanation:

`f(x)= (x^2+4x-3)/(x-6)`

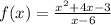
To find out vertical asymptote , we take the denominator and set it =0

x-6=0 , so x=6

Vertical asymptote at x= 6

The degree of numerator is 2 and the degree of denominator is 1.

Here, the degree of numerator is higher than the degree of denominator. So there will be a slant or oblique asymptote. we can find it by long division.

x + 10

-------------------------------

x-6 x^2 + 4x -3

x^2 - 6x

-------------------------------(subtract)

10x - 3

10x - 60

-----------------------------(subtract)

57

Oblique asymptote at y=x+10

Answer 2

vertical asymptote: x=6

Horizontal asymptote: doesn't exist.

Explanation:

Given function is
`f\left(x\right)=(x^2+4x-3)/(x-6)`

To find vertical asymptote, we just set denominator =0 and solve that for x

Given denominator is x-6

then x-6=0

or x=6

Hence vertical asymptote: x=6

-----

We see that degree of numerator = 2

degree of denominator = 1

When degree of numerator is not equal to degree of denominator then horizontal asymptote doesn't exist.

Horizontal asymptote: doesn't exist.