Answer:
Additive inverse is
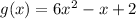
Explanation:
We have the function
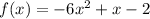 .
.
Now, for the additive inverse, we have the property that, there exists a function g(x) such that f(x)+g(x) = g(x)+f(x) = 0.
So, we have,
f(x)+g(x) = g(x)+f(x) = 0
i.e.

i.e.
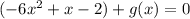 and
and
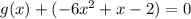
i.e.
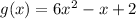 and
and
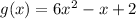
i.e.
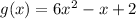
Thus, the additive inverse of
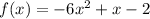 is
is
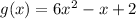 .
.