Question

A spherical ball is inflated so that it’s radius increases in the ratio 4:3. Find the ratio in which it’s volume is increased

Answer 1

by a factor of 64/27 or 64:27

Explanation:

Volume of a sphere = 4/3 pi r^3

now increase the radius by 4/3 ( this is 4:3)

new volume = 4/3 pi (4/3 r)^3

= 64/27 * 4/3 pi r^3

so the original volume is increased by 64/27

Answer 2

64:27

Explanation:

If the ratio between the old and new radius is described with the ratio: 4:3, then if the first radius was 3, then the new radius is 4.

Also if you multiply 3 by (4/3) it also equals 4

The volume of a sphere is described as:
`(4)/(3) \pi r^(3)`

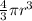
So let's plug in 3 and 4 and see their ratio.

`((4)/(3)\pi 4^(3) )/( (4)/(3)\pi 3^(3) )} = (4^(3) )/(3^(3) ) = (64)/(27)`

The answer is 64/27 or (4/3)^3