Question

The elk population in an area is increasing. This year, the population was 1.076 times last year's population of 1537.

Assuming that the population increases at the same rate for the next few years, write a formula for the sequence. ( HINT: The beginning elk population for your equation is not 1537...that was last year's herd size.) Then find the expected elk population after nine years.

Answer 1

Original Population of elk= 1537

Population after a year =1537 × 1.076

Let rate at which Population of elk is increasing = R %

Let In the beginning the population of elk= P

t= Time after which population is to be found

E(x)=Population of elk after time t,that is E(0)=P

So, Writing the formula at the rate which population of elk is increasing:

⇒E(x)=
`P(1 +(R)/(100))^t`

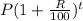
E(1)= 1537

⇒1537=
`P(1 +(R)/(100))^1`

1537=
`P(1 +(R)/(100))`

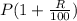
E(2)= 1537 × 1.076=1653.812

⇒ 1653.812=
`1537(1 +(R)/(100))^1`

`(1653.812)/(1537)=(1 +(R)/(100))^1\\\\ (1.076) =(1 +(R)/(100))\\\\ 1.076-1=(R)/(100)\\\\ 0.076 * 100= R \\\\ R= 7.6`

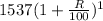
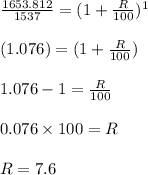
E(9)= 1537
`*(1+(R)/(100))^8`

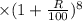
As P is population when t=0, so we have to find population after 9 years , as
`P_(1)` is population when t=1,so considering
`P_(1)` as initial population, so, t=8

E(9)=
`1537 * (1.076)^8`

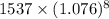
= 1537 × 1.796

= 2761.6716

= 2761.68 (Approx)