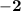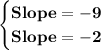SOLVING
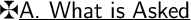
Calculate the slope of the line between each pair of co-ordinates


The points given are,
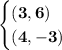
To find the slope
 of this line,
of this line,
we will utilise the
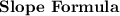 .
.
The first thing to do is
to put in the co-ordinates
of the two points given.
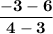 | subtract on top and bottom
| subtract on top and bottom
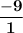 | divide on top and bottom
| divide on top and bottom


The points given this time are,
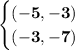
Last time we needed to
put in the co-ordinates.
Similarly, we ought to
put in the co-ordinates
in this problem.
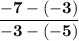 | simplify
| simplify
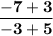 | add on top and bottom
| add on top and bottom
 | divide on top and bottom
| divide on top and bottom