Question

Help Please!!

Match the graph with the correct equation.


y + 2 = (x – 2)


y – 2 = –(x – 4)


y + 2 = –(x – 4)


y + 2 = –(x + 4)

Answer 1

Hey there! My name if Fatima Berry ❤

Answer: y+2 = -(x-4)

Explanation:

The first step is to change the equations into y format. y= mx + b.

The y- intercept of this graph is at the point (0,2). Since the line is going down, the slope is negative. Therefore it would be: y+2 = -(x-4)

If changed it would be y= -x + 2.

Hope it help

Answer 2

The required equation is y+2=-(x-4), therefore the correct option is 3.

Explanation:

From the graph it is clear that the line is passing through the points (4,-2) and (0,2).

The slope of the line is

`m=(y_2-y_1)/(x_2-x_1)=(2-(-2))/(0-4)=-1`

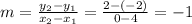
The slope of the line is -1.

The point slope form of a line is

`y-y_1=m(x-x_1)`

`y-(-2)=-1(x-(4))`

`y+2=-(x-4)`

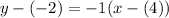
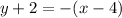
The required equation is y+2=-(x-4), therefore the correct option is 3.