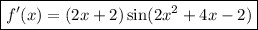It depends if you mean
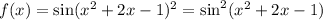
i.e. the sine part is getting squared, or
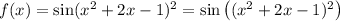
i.e. the argument to sine is getting squared. I'll assume the first case, since it's fairly common convention to write
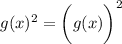 .
.
Now if
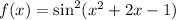
• by the power and chain rules we have
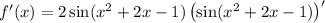
• using the derivative of sine and the chain rule again we have
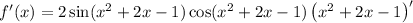
• with the power and chain rules we have
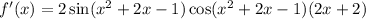
Recalling the double angle identity for sine,
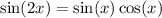
we can rewrite the derivative among several other ways as