Question

Suppose you need to get the dent in your car fixed. You see the ads in the newspaper above (mikes repair shop $100 service charge plus $65 per hour) and (Amy’s auto repair $40 service charge plus $80 per hour) your father, who knows a bit about cars, said it would take no more than 3 hours for the repair person to fix your car. How do you determine where you should take your car to get it repaired? Let x = number of hours worked on, and Let y = total cost to you. Use substitution or elimination method to find the point of intersection

Answer 1

Total Cost at Amy's shop is $280 which is less than the total cost at Mike's shop which is $295, so I will take the car to Amy's shop

Point of intersection: (x,y) = (4,360)

Step-by-step explanation:

Part 1 )

Let x = number of hours worked

Let y = total cost to you

Determining where to take the car:

Total Cost at Amy's shop is $280 which is less than the total cost at Mike's shop which is $295

Mike's repair shop:

Service fee: $100

Per hour rate: $65

Let x is the number of hours worked on. Total cost will be equal to the service fee plus hourly charges. Charges per an hour are $65, so for x hours the charges will be 65x.

Therefore, total cost for Amy's repair shop can be written as:

y = 100 + 65x ------(1)

For 3 hours work: y = 100 + 65(3)

Cost at Mike's, y = $100 + $195 = $295

Amy's repair shop:

Service fee: $40

Per hour rate: $80

Charges per an hour are $40, so for x hours the charges will be 80x.

Therefore, total cost for Amy's repair shop can be written as:

y = 40 + 80x ------(2)

For 3 hours work: x = 3

y = 40 + 80(3)

Cost at Amy's, y = $40 + $240 = $280

Part 2)

Find the point of intersection

Using elimination method:

y = 100 + 65 x ------1

y = 40 + 80x ------2

As the y coefficients are equal we will subtract eq1 from eq2

y - y = 40 + 80x - 100 - 65x

0 = -60 + 15x

60 = 15x

x =
`(60)/(4)`

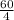
x = 4

put x = 4 in eq 1

we get y = 100 + 65 (4) = 100 + 260 = 360

x = 4, y = 360

Point of intersection: (x,y) = (4,360)